Proyecto «Angarmegia: Ciencia, Cultura y Educación». Portal abierto y colaborativo de Investigación y Docencia

/

Cuando una igualdad algebraica se verifica siempre, cualquiera que sea el valor numérico de las letras o las variables, se denomina IDENTIDAD. Si la igualdad se cumple sólo para algunos valores de las letras o las variables, la igualdad se denomina ECUACIÓN. Por ejemplo:

x(a + b)= ax + bx

Es una IDENTIDAD: Se cumple cualesquiera que sean los valores de a, b o x.

4x-2y=2

Es una ECUACIÓN: Sólo se cumple cuando x=5 e y=9.

La solución de problemas de ecuaciones requiere de la formulación de un modelo numérico que refleje, mediante la combinación adecuada de los datos conocidos y desconocidos buscados (incógnitas), en un conjunto de operaciones numéricas e igualdades cuyo cálculo suministrará la información buscada. Es lo que se conoce como PLANTEAMIENTO DEL PROBLEMA. Una vez planteada correctamente la cuestión, la solución se alcanza fácilmente actuando con rigor y método.

Enunciado:

A una representación escolar acuden 450 persona. El número de niños triplica al de madres, mientras que los padres solo suman la mitad de ellas. ¿Cuántos padres, madres y niños acuden al evento?

PLANTEAMIENTO
Incógnita principal:

Número de madres:  x

Datos conocidos:

Total de asistentes:  450

Número de niños: 3x

Número de padres:

Número de niños: 3x

Resolución

Eliminar dedominadores

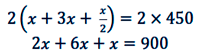
Reducir términos

9x = 900

Despejar la incógnita principal

Cálculo de otras incógnitas

Niños: 3x = 3 x 100 = 300

Padres: =

SOLUCIÓN DEL PROBLEMA:
100 madres - 300 niños - 50 padres

Enunciado:

Dos inversores adquieren acciones de dos empresas distintas. La compra de “A” asciende a 2.000 euros, mientras que la inversión de “B” es de 10.000 euros. Ambos obtienen el mismo
beneficio, pero entonces “B” tiene tres veces más dinero que su compañero. ¿Qué cantidades ganaron?

PLANTEAMIENTO
Incógnita principal:

Ganancia: x

Datos conocidos:

Capital final A: 2.000 + x

Capital final B: 10.000 + x

Ecuación final: 3(2.000 + x) = 10.000 + x

Resolución

Suprimir paréntesis

(3 x 2.000) + 3x = 10.000 + x

6.000 + 3x = 10.000 + x

Transponer términos

3x - x = 10.000 - 6.000

Reducir términos

2x = 4.000

Despejar la incógnita principal

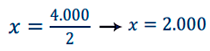
SOLUCIÓN DEL PROBLEMA:
Cada inversor obtiene un beneficio de 2.000 euros

Enunciado:

Una herencia se distribuye de la siguiente manera: La mitad del dinero será para la esposa, la tercera parte para el hijo y la décima parte para una sobrina. Si, además, quedan 20.000 euros para una obra benéfica, ¿a cuánto asciende la cantidad a repartir?

PLANTEAMIENTO
Incógnita principal:

Total de la herencia = x 

Datos conocidos:

Herencia de la esposa:

Herencia del hijo:

Herencia de la sobrina:

Herencia obra benéfica: 20.000 euros

Ecuación final:

Resolución

Eliminar denominadores:

m.c.m.(2, 3, 10) = 30x

30x = 15x + 10x + 3x  + 600.000

Transponer términos

30x - 5x - 10x - 3x = 600.000

Reducir términos

2x = 600.000

Despejar la incógnita principal

Cálculo de otras incógnitas
Esposa: 

Hijo: 

Sobrina: 

SOLUCIÓN DEL PROBLEMA:
Esposa: 150.000 euros – Hijo: 100.000 euros – Sobrina: 30.000 euros

Enunciado:

Un padre tiene 49 años y su hijo 11. ¿Cuántos años han de transcurrir para que el padre triplique la edad del hijo?

PLANTEAMIENTO
Incógnita principal:

Años transcurridos = x 

Datos conocidos:

Edad del padre pasados x años: 49 + x

Edad del hijo pasados x años: 11 + x

Ecuación final: 49 + x = 3(11 + x)

Resolución

Efectuar paréntesis:

49 + x = 33 + 3x

Transponer términos

-3x + x = 33 - 49

Reducir términos

-2x = -16

Despejar la incógnita principal

SOLUCIÓN DEL PROBLEMA:
Tiempo transcurrido: 8 años

ADEMÁS