Proyecto «Angarmegia: Ciencia, Cultura y Educación». Portal abierto y colaborativo de Investigación y Docencia

/

Se encuadra bajo el nombre de regla de tres al método aritmético que resuelve aquellos problemas en los que intervienen magnitudes directa o inversamente proporcionales de las que se conocen dos cantidades de la primera y una de las correspondientes de la segunda, y se solicita calcular la que falta para completar la proporción. El tipo más sencillo corresponde al modelo:

Si 15 m de tejido cuestan 1800 euros, ¿cuánto importará una pieza de 300 metros?

En toda regla de tres hay varios elementos: supuesto, pregunta, cantidades principales y cantidades relativas. 

En el problema de ejemplo propuesto más arriba, la transcripción sería la siguiente: 

La regla de tres puede ser simple, si el problema depende de una sola proporción, o compuesta, cuando depende de dos o más proporciones. Además, de acuerdo con la condición de las magnitudes que intervienen en la cuestión, será directa o inversa.

Paso 1: Plantear

Escribir los datos suministrados por el enunciado en dos líneas diferentes, primero el supuesto y debajo la pregunta, de modo que correspondan en columna las cantidades principales y las relativas. Ya se hizo con el problema ejemplo. Se repite a continuación y se prosigue con el proceso para su mejor comprensión.

Paso 2: Identificar el tipo de proporcionalidad 

Determinar si la relación existente entre las dos magnitudes es de proporcionalidad directa o inversa.

Paso 3: Concretar la proporción. 

Definir las razones entre las cantidades principales y relativas del supuesto y la pregunta.   Establecer la proporción igualando ambas razones teniendo en cuenta:

·         Si la proporcionalidad es directa  se igualan, sin más, ambas razones.

·         Si la proporcionalidad es inversa se iguala una razón con la inversa de la otra. 

Razón inicial (Según enunciado)

Razón final (En  función del tipo de proporcionalidad)

Paso 4: Despejar la incógnita

Aplicar la propiedad fundamental de las proporcione para calcular la incógnita:

·         Cálculo de un extremo: Producto de los medios dividido entre el otro extremo.

·         Cálculo de un medio: Producto de los extremos dividido entre el otro medio.

La solución de un problema de regla de tres simple inversa, sigue el exactamente el mismo procedimiento: 

• Fase 1: Plantear

• Fase 2: Identificar tipo de proporcionalidad

• Fase 3: Establecer la proporción

• Fase 4: Despejar la incógnita

Sólo hay que tener en cuenta en el momento de establecer la proporción la necesidad de invertir una de las dos razones que se definen en el problema.

A continuación se resuelven varios problemas de proporcionalidad inversa para fijar esta cuestión.

Ejemplo 1: Cuatro obreros necesitaron veinte días para terminar un trabajo. ¿Cuántos días habrían invertido diez hombres en realizar la misma tarea?

Razón inicial (Según enunciado) - Obreros

Razón inicial (Según enunciado) - Días

Razón final. (En  función del tipo de proporcionalidad)

Solución:

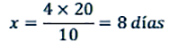
Ejemplo 2: Un estudiante empleó 25 días en terminar un libro recomendado por su profesor leyendo 36 páginas cada día. Su compañero sólo pudo avanzar 20 páginas diarias en la lectura del mismo libro. ¿Cuánto tiempo tardó en completar su tarea escolar?

Razón inicial (Según enunciado) - Páginas

Razón inicial (Según enunciado) - Días

Razones finales (En  función del tipo de proporcionalidad) - Páginas/ Días

Solución:

Ejemplo 3: Un manantial que proporciona 180 litros de agua por minuto llena los depósitos de abastecimiento de una población en 14 horas. ¿Cuánto tardaría si el caudal fuese de 70 litros por minuto?

Razón inicial (Según enunciado) - Principal

Razón inicial (Según enunciado) - Relativa

Razones finales (En  función del tipo de proporcionalidad) - Principal/Relativa

Solución:

ADEMÁS