|
|
|
|
|
|
DIRECTORIO de la SECCIÓN |
PROBLEMAS |
|
Los documentos a los que desde aquí se accede han sido realizados expresamente para desarrollar los programas académicos que trabajamos con nuestros alumnos. También está disponible una estructura tipo «Wiki» colaborativa, abierta a cualquier docente o alumno que quiera participar en ella. Para acceder a estos contenidos se debe utilizar el «DIRECTORIO de la SECCIÓN». Para otras áreas de conocimiento u opciones use el botón: «Navegar» |
|
|
Razonamiento y planteamiento |

|
Problema 1 |
Se incrementa un número en cuatro unidades y se disminuye también en cuatro unidades. Si se multiplican entre sí estos resultados se obtiene 609. ¿Cuál es el número original?
Planteamiento
Incógnita principal:
Número buscado = x
Datos conocidos:
Número incrementado = x + 4
Número disminuido = x - 4
Producto de ambos números = x + 4 × (x-4) = 609
Ecuación final:
x2 - 16 = 609
x2 - 625 = 0
|
Problema 2 |
Se precisa encontrar las dimensiones de un rectángulo de 2520 m2 de superficie sabiendo que su longitud excede en 18 m a su anchura.
Planteamiento
Incógnita principal:
Anchura del rectángulo = x
Datos conocidos:
Área del rectángulo = longitud * ancho
Longitud del rectángulo = x + 18
Superficie del rectángulo = m2
Ecuación final:
(x + 18) x = 2520
x2 + 18x - 2520 = 0
|
Problema 3 |
La diferencia entre dos números es 14. Si la suma de sus cuadrados asciende a 436, ¿de qué números se trata
Planteamiento
Incógnita principal:
Número mayor = x
Datos conocidos:
Número menor = x - 14
Número mayor2 = x2
Número menor2 = (x - 14)2
Suma de cuadrados = 436
Ecuación final:
x2 + (x - 14)2 = 436
2x2 - 28x - 240 = 0
|
Problema 4 |
El área de un rectángulo es de 1000 m2. Si su perímetro mide 140 m, ¿cuáles son sus dimensiones?
Planteamiento
Incógnita principal:
Lado a = x
Datos conocidos:
Área rectángulo = a * b = 1000 m2
Semiperímetro = a + b = 70 m2
Lado b = (70 - x)
Ecuación final:
x (70 - x) = 1000
-x2 + 70x - 1000 = 0
|
Problema 5 |
La altura de un triángulo mide la tercera parte de la longitud de su base. Si el área del triángulo es de 4225 m2, ¿cuánto mide su base?
Planteamiento
Incógnita principal:
Base = x
Datos conocidos:
Altura =
![]()
Área =
![]()
Ecuación final:
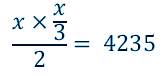
![]()
ADEMÁS
|
Responsables últimos de este proyecto Antonio García Megía y María Dolores Mira y Gómez de Mercado Son: Maestros - Diplomados en Geografía e Historia - Licenciados en Flosofía y Letras - Doctores en Filología Hispánica |
|
Apunte estadístico Portal activo desde abril de 2004. Los auditores de seguimiento que contabilizan las visitas desde esa fecha acreditan una suma entre 4.000 y 10.000 visualizaciones diarias para el conjunto de secciones que lo integran. Las visitas en el servidor «https» son privadas y no quedan reflejadas en los contadores visibles |
|
|