|
|
|
|
|
|
DIRECTORIO de la SECCIÓN |
MAGNITUDES PROPORCIONALES |
|
Los documentos a los que desde aquí se accede han sido realizados expresamente para desarrollar los programas académicos que trabajamos con nuestros alumnos. También está disponible una estructura tipo «Wiki» colaborativa, abierta a cualquier docente o alumno que quiera participar en ella. Para acceder a estos contenidos se debe utilizar el «DIRECTORIO de la SECCIÓN». Para otras áreas de conocimiento u opciones use el botón: «Navegar» |
|
|
Concepto y medida |
Se denomina magnitud a todo aquello
que es susceptible de medida. Para medir
se procede a comparar la magnitud con otra fija similar, definida y acordada
previamente como patrón, llamada unidad,
para averiguar cuántas veces la contiene.
La medida se representa mediante un número que establece el resultado de la
comparación. Si un objeto mide tres metros, la cantidad,
3 m, indica que es
tres veces mayor que la unidad
establecida para medir longitudes, el
metro.
La bondad, al amor o el odio, no se pueden cuantificar a través de una medida,
por los tanto, no son magnitudes. La temperatura, la velocidad, la masa, el
peso…, por el contrario, sí son magnitudes.
|
Magtitudes y unidades
principales |
||
|
Magnitud fundamental |
Unidad |
Abreviatura |
|
m |
||
|
kg |
||
|
s |
||
|
K |
||
|
A |
||
|
cd |
||
|
mol |
||
Clases de
magnitudes
Dos magnitudes se dice que son directamente proporcionales si se relacionan de modo qu
Son ejemplo de magnitudes directamente proporcionales número de artículos y precio o velocidad y camino recorrido.
Ejemplo de magnitudes directamente proporcionales
|
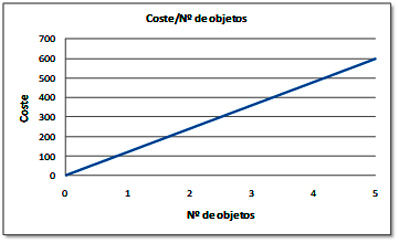
Proporcionalidad directa
Número de artículos/precio a pagar |
|
|
Cantidad |
Precio |
|
1 |
120 |
|
2 |
240 |
|
3 |
360 |
|
4 |
480 |
|
5 |
600 |
Representación gráfica
Dos magnitudes se dice que son
inversamente proporcionales si se
relacionan de modo que:
A cada cantidad de la primera le corresponde otra de la segunda, y
recíprocamente.
Si se multiplica una cantidad de la primera por un número, la cantidad
correspondiente de la segunda queda dividida entre el mismo número, es
decir, si a doble, triple... cantidad de la primera, corresponde mitad,
tercio... de la segunda.
Son
ejemplo de magnitudes inversamente proporcionales el número de obreros
encargados de realizar una obra y el tiempo invertido en terminarla o velocidad
y el tiempo empleado en recorrer una misma
distancia.
Ejemplo de magnitudes inversamente proporcionales
|
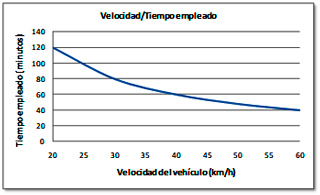
Proporcionalidad inversa
Velocidad/tiempo invertido en un trayecto |
|
|
Velocidad |
Tiempo invertido |
|
20 km/h |
120 minutos |
|
30 km/h |
80 minutos |
|
40 km/h |
60 minutos |
|
50 km/h |
48 minutos |
|
60 km/h |
40 minutos |
Representación gráfica
ADEMÁS
|
Responsables últimos de este proyecto Antonio García Megía y María Dolores Mira y Gómez de Mercado Son: Maestros - Diplomados en Geografía e Historia - Licenciados en Flosofía y Letras - Doctores en Filología Hispánica |
|
Apunte estadístico Portal activo desde abril de 2004. Los auditores de seguimiento que contabilizan las visitas desde esa fecha acreditan una suma entre 4.000 y 10.000 visualizaciones diarias para el conjunto de secciones que lo integran. Las visitas en el servidor «https» son privadas y no quedan reflejadas en los contadores visibles |
|
|